comes from now that you know! Include all appropriate terminology (secant line, tangent line, h/delta x, etc). Your post must include text and some form of media (picture/video) to support your writing.
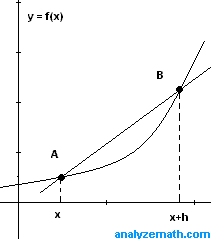
The Difference Quotient can be explained as we are attempting to find the tangent line in a function on a graph. First we will have a curved line that has a secant line that will touch the graph twice and a tangent line that will only touch it once. At the farthest point of intersection, we will use dx to solve for the secant line and labeling it as h. As we see that the secant line is no where near the tangent line, the equation is f(x+dx)-f(x)/dx. We need to find the value for the secant line that is closer to the tangent line. We can make dx smaller so that the secant line is barely touching the tangent line. The slope of the secant line can be described as the difference quotient, we can find the slope by using the slope formula which is m=y2-y1/x2-x1. Then we can plug in the x-value (x+h) and then the y-value (f(x+h)) the new equation would be (f(x+h)-f(x))/(x+h)-x)). As we simplify this function we see that f(x+h)-f(x) does not simplify. Then we use lim-->0 to show that the secant line and the tangent line cannot touch.
Here is an example of how the difference quotient turns out to be, A being the tangent and B the secant:
This video explains the Difference Quotient:
Links used:
http://www.analyzemath.com/calculus/Differentiation/difference_quotient_1.gif
http://www.youtube.com/watch?v=XA0fZh8cXV8
No comments:
Post a Comment