Parabola

1) What is the mathematical definition of this conic section and how does that definition play a role in the properties of the conic section and how it is shaped or formed?

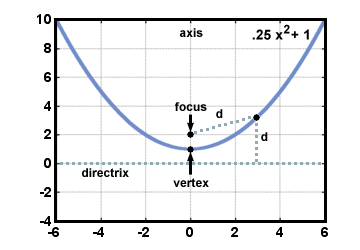
-The mathematical definition of a parabola is shown by referring to the focus, drawing a line from the focus to any point on the parabola, should be equal to a line drawn straight down in a perpendicular matter starting from that same point to the directrix. "P" is the key component that describes how the parabola will look like in shape, form, and direction it opens up to.
This will determine in which direction the graph will open up:
+p x^2 Graph opens up
+p y^2 Graph opens right
-p x^2 Graph opens down
-p y^2 Graph opens left














2) How does the focus (foci) affect the shape of the conic section?

- "P" determines a major portion of the graph. It shows where the parabola opens up and shows how "fat" or  "skinny" the graph really is. If "p" equals a large number then the graph will be fairly large and "fat", if it is a smaller number then it determines that the graph will be small or "skinny".


3) How do the properties of this conic section apply in real life?

-With its parabolic shape and a focus a parabaloid can be used in many different situations.One that I found interesting was the parabolic mirror, this mirror can generate almost 2,000 kilowatts of solar energy. Although it is impractical the mirror can heat objects quickly due to its concave shape and focus in the middle. Solar energy is concentrated in the center and is emitted forward and focused. This video explains its many uses:  

Additional information about parabolas!: http://www.purplemath.com/modules/parabola.htm

Works Cited:

http://jwilson.coe.uga.edu/emt668/EMAT6680.2003.fall/Burrell/EMAT%206680/Assignment%202/image65.gif
http://img.sparknotes.com/figures/B/b3c3339e9dd544eae6e9167beedc1b9e/parabola.gif
http://youtu.be/1RNNlYiKxlc
http://www.purplemath.com/modules/parabola.htm