WPP 10

Create your own Playlist on MentorMob!

Create your own Playlist on MentorMob!

Create your own Playlist on MentorMob!

Fibonacci Haiku

Sachi
I...
I'm sorry.
I was weak.
I could not save you.
My heart aches without you by my side.
Ever since that day I have been lost without you... please forgive me.

Unit K Student Problem 7

In this problem I created a repeating decimal and solved it to be a rational fraction. First I started by listing the repeating numbers, then I proceeded to find a1 and "r". To find a1 it is the first number that I listed and converted it to a fraction, to find "r" I divided the first term by the second. Next, I then wrote out my infinite summation formula plugging in the a1 and "r" as i go. To solve for the geometric series the formula is:  "a" sub 1 divided by 1 minus "r". After plugging in the numbers and solving I notice that the equation has a number in front of the decimal. To solve for this simply add the number to the fraction that you had received to solve for the rational fraction of the repeating decimal.

Unit J Student Problem 6

In this unit I created and solved a problem for PFD which stands for Partial Fraction Decomposition. First I start by adding the numerators together via Algebra 2 skill in which I multiply the numerators and the denominators by which terms they are missing from the denominator. After I have done that I then separate the original problems using variables such as A,B,and C for the numerator instead of the original numbers. I then make the common denominator the same way i did to the previous step. The next step is to add all the like terms and put them equal to the numerator that I have found when I solve for the common denominator. After you remove the x^2 and x so that you can solve for A,B, and C.I notice that there is one variable that I can easily solve for, I solve for it. Before I plug in the variable that I already have I first eliminate a variable from the two previous equations. I do this by multiplying a constant if needed. After I have removed a variable I can now plug in the term that I had found earlier and solve for the second term. I now have two terms and can plug both of them into any of the original three equations that I have constructed. After plugging them in and solving for the last variable I can check my answer if it matches the original equation that I had constructed in the beginning of the problem.

Unit J Student Problem 5

In this unit I created and solved a problem for PFD which stands for Partial Fraction Decomposition. First I start by adding the numerators together via Algebra 2 skill in which I multiply the numerators and the denominators by which terms they are missing from the denominator. After I have done that I then separate the original problems using variables such as A,B,and C for the numerator instead of the original numbers. I then make the common denominator the same way i did to the previous step. The next step is to add all the like terms and put them equal to the numerator that I have found when I solve for the common denominator. After you remove the x^2 and x so that you can solve for A,B, and C.I notice that there is one variable that I can easily solve for, I solve for it. Before I plug in the variable that I already have I first eliminate a variable from the two previous equations. I do this by multiplying a constant if needed. After I have removed a variable I can now plug in the term that I had found earlier and solve for the second term. I now have two terms and can plug both of them into any of the original three equations that I have constructed. After plugging them in and solving for the last variable I can check my answer if it matches the original equation that I had constructed in the beginning of the problem.

Unit I WPP#6

Create your own Playlist on MentorMob!

Unit I Student Problem 4

Unit I Student Problem 3

Student Video 3: Unit H Concept 7

In this video Brian V. and I constructed a problem on Unit H Concept 7. We briefly describe and show how to solve for logs given the approximation.

Unit G Question 1

1) How do we know that a graph has a horizontal asymptote? What are the three options?

- This means that the Asymptote is equal to zero this is because “x” has to be zero because it is supposed to be a horizontal line. “Y” is all real numbers. Also if the degree is bigger on the top then the asymptote will equal zero. If the degree is the same then the asymptote is the ratio of  the coefficients. And if the degree is bigger on top then there is no horizontal asymptote. The limit notation for horizontal asymptotes corresponds with the restrictions that we did on Unit E Concept 4 This shows the behavior in which the graph is corresponding to the equation.

Unit G Question 2

2) Describe what limit notation for a horizontal asymptote actually means.

- The limit notation for a horizontal asymptote means that the behavior of the graph varies depending on its degree. This shows how the graph moves depending on the right side or the left. The graph tells how close or   far away the asymptote is from the graph itself. You can find the limit notation easily after you have compared the graph's numerator and denominator. If it is bigger on bottom then the asymptote is zero. If it is the same degree then you must use the ratio of the coefficients. If the asymptote is bigger on the top then there is no asymptote.

Unit G Question 3

3) When does a graph has a slant asymptote? How do you find the equation of a slant asymptote?

- A graph has a slant asymptote when only the degree on top is bigger than the degree on the bottom. We can find a slant asymptote by using long division. Everything but your remainder will become the equation of the slant asymptote line. The equation of a slant asymptote is the same as slope intercept form with Y=mx+b.

Unit G Question 4

4) What is the difference between a graph having a vertical asymptote and a graph having a hole?

- A graph that has a vertical asymptote has nothing that can cancel out in the original function. The asymptote also goes straight down with no interference. While a graph with holes has something that can cancel out in the original equation. This will have an affect on the graph as there will be some interference with the graph or as we call holes.

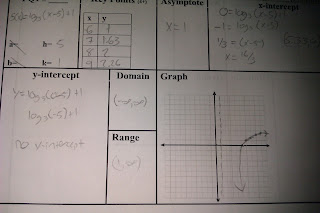
Unit G Question 5

5) Describe the conditions in which a graph can cross through an asymptote.

- Graphs can only sometimes cross through an asymptote. However it has to meet certain requirements before doing so. One is that graphs can only cross towards the middle of the graph and never towards the far left or far right.

Unit G Question 6

6) How do we find the appropriate place to plot a hole if the y-value is undefined when plugged into the original equation?

- To find the holes after finding it in the original equation, you can use a calculator to find the holes. To use the calculator you must plug in the original equation to see the graph. Then you must bring out the table in your graphing calculator. After you can scroll down and see which plotted points are undefined.

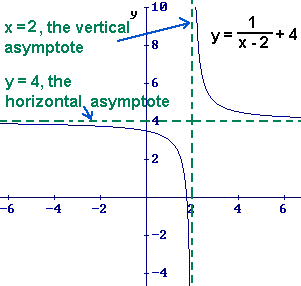
Unit G Question 7

7) Describe how to write limit notation for vertical asymptotes and what the notation means.

- Limit notation for vertical asymtotes deviates from the standard limit notation for polynomials. First you must find the zeros for the denominator of the original equation. After you have found the zeros then you set up the limit notation with "as x >#, F(x)>(+/-)inf" and vice versa. For the limit notation for vertical asymptotes you must look at where the graph moves from the right and also from the left.

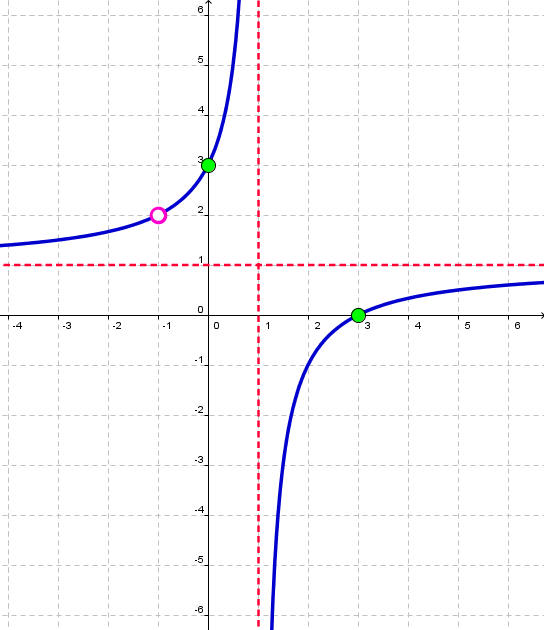
Unit G Question 8

8) How do you find the y-intercept of a rational function? Does this need to be done in the original or simplified equation?

- To find the y-intercept for a rational function you must first factor out the original equation. After you have it factored out (you must use the factored equation) you will set the equation equal to y and replace all the x's with zeros.

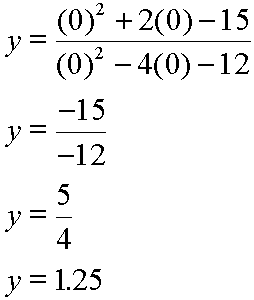
Unit G Question 9

9) Describe how to find the x-intercepts of a rational function. Include both the long way and the shortcut way, explaining why the shortcut makes mathematical sense.

- To find the x-intercepts of a rational function you must first factor out the regular equation. After you will plug in zero for "y". For the long way you must multiply the equation by its denominator. This will eliminate the denominator so it will be easier to solve for zero. The shortcut is to just set the numerator equal to zero. This is because if you think about it eliminating the denominator will take more work if you already know that it will cancel.

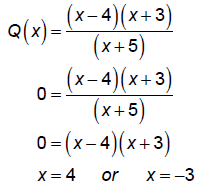
Unit G Question 10

10) While the domain of a rational function depends on DIVAH, what do you think the range of a rational function depends on? Give an example.

- I believe that if a domain depends on the vertical asymptotes and its holes then the range will depend on its horizontal asymptotes. This is because the x-axis depends on its vertical line and the y-axis depends on its horizontal line so that you can actually see the asymptotes. 

Unit F Concept 10 Student Video